Yleisimpien tietorakenteiden operaatioiden aikavaativuudet
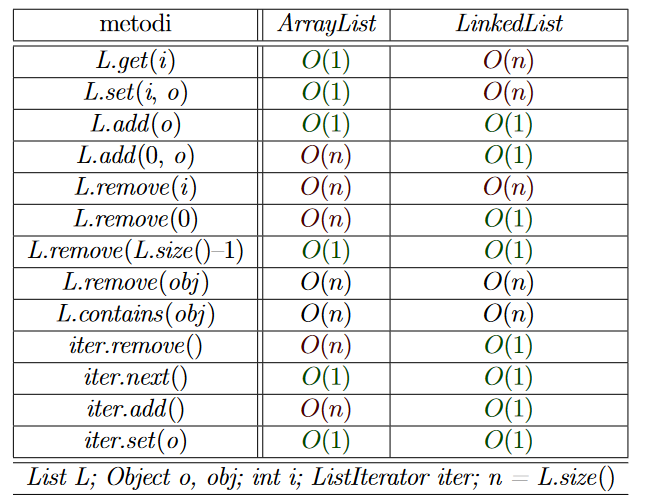
| List | Add | Remove(i / obj) | Get | Set | Contains | Next | Data Structure |
|---|---|---|---|---|---|---|---|
| ArrayList | O(1) | O(n) | O(1) | O(1) | O(n) | O(1) | Array |
| LinkedList | O(1) | O(n) | O(n) | O(n) | O(n) | O(1) | Linked List |
| Queue | Offer | Peak | Poll | Remove | Size | Data Structure |
|---|---|---|---|---|---|---|
| PriorityQueue | O(log n) | O(1) | O(log n) | O(n) | O(1) | Priority Heap |
| LinkedList | O(1) | O(1) | O(1) | O(1) | O(1) | Array |
| ArrayDequeue | O(1) | O(1) | O(1) | O(n) | O(1) | Linked List |
| Set | Add | Remove | Contains | Next | Size | Data Structure |
|---|---|---|---|---|---|---|
| HashSet | O(1) | O(1) | O(1) | O(h/n) | O(1) | Hash Table |
| LinkedHashSet | O(1) | O(1) | O(1) | O(1) | O(1) | Hash Table + Linked List |
| EnumSet | O(1) | O(1) | O(1) | O(1) | O(1) | Bit Vector |
| TreeSet | O(log n) | O(log n) | O(log n) | O(log n) | O(1) | Red-black tree |
| Map | Get | ContainsKey | Next | Data Structure |
|---|---|---|---|---|
| HashMap | O(1) | O(1) | O(h / n) | Hash Table |
| LinkedHashMap | O(1) | O(1) | O(1) | Hash Table + Linked List |
| TreeMap | O(log n) | O(log n) | O(log n) | Red-black tree |
Peräkkäisrakenteet
Helppoja ja tehokkaita oikein käytettyinä
Linkitetty Lista
- Käytetään iteraattorilla tai toteutuksen operaatioilla.
+peräkkäiseen läpi käymiseen+keskelle lisäämiseen-etsimiseen
pino
- last in first out
Avopino
- muutama ylin voidaan tarkastaa
Jono
- first in first out
Pakka
- lisäys ja poisto molemmista päistä
Rengas
- päillä ei ole väliä
- viimeisestä next() on ensimmäinen
Taulukko
- Käytetään indeksillä
+etsiminen+indeksiin viittaaminen-lisääminen (loppu ok)-poistaminen (loppu ok)
ArrayList
- Toteuttaa listan operaatiot taulukon aikavaativuuksin
Vector
- tukee säikeitä
Puut
Kaikkien operaatioiden aikavaativuus tehokkaassa toteutuksessa on O(1)
Binääri Puu
Tasapainotettu binääripuu
+etsiminen logaritmista
Yleinen Puu
- rajaton määrä lapsia
Muita puita
- ALV puu
- Punamusta puu
- B-puu
Joukot
- Ei duplikaatteja (samoja alkioita)
- läpikäynti
- for each
- while + lopetusehto
- iteraattori
HashSet
- add, remove, contains O(1)
- Joukko-operaatiot O(n)
LinkedHashSet
- läpikäynti lisäys järjestyksessä
TreeSet
- Joukko-operaatiot O(n log(n))
NavigableSet
- läpikäynti takaperin ja muuta mukavaa
Sanakirjat
Vain yhtä joukkoa hallitsevaa kokoelmaa sanotaan sanakirjaksi
- Avain
Relaatio
???
Kuvaus
- Yleisen joukon erityistapaus
- Key / Value -parit
- containsKey() O(1)
- containsValue() O(n)
HashMap
TreeMap
Monilista
??
PrioriteettiJono
Määritellään joukon alkioille prioriteetti (tärkeysjärjestys, kiireellisyysjärjestys)
Laukku
Sama alkio useasti kokoelmassa
Verkot - Graphs
Useita seuraajia ja edeltäjiä
Läpikäynti
Solmujen värjääminen
Syvyyssuuntainen läpikäynti
- Aikavaativuus
O(n+e)jossa n=solmujen mnäärä ja e=kaarten määrä Kaarten luokittelu syvyyssuuntaisessa läpikäynnissä
Puukaari
Johtavat käsittelemättömiin solmuihin
Paluukaari
Johtavat solmusta esi-isään
Etenemiskaari
Johtavat solmusta jälkeläiseen
Ristikkäiskaari
Eivät johda esi-isään eivätkä jälkeläiseen
Verkon algoritmeja
Primin algoritmi
Aikavaativuus O(eloge)
Pahimmassa tapauksessa O(n²logn)
Kruskaalin algoritmi
Aikavaativuus O(eloge)
Dijkstran algoritmi
Aikavaativuus O()
Suuntaamattoman verkon läpikäynti
Leveyssuuntainen läpikäynti
käsitellään kaikki solmun naapurit -> käsitellään kaikki naapureiden naapurit
Syvyyssuuntainen läpikäynti
käsitellään kaikki solmun naapurin naapurit ennen seuraavan solmun naapurin kääsittelyä vrt. puun läpikäynti sisäjärjestyksessä
Käsitteitä
- Minimi leikkaus - painoltaan pienin joukko kaaria, jotka poistamalla verkko saadaan jaettua kahtia.
- leikkaus solmu - yksittäinen solmu, joka erottaa verkon osat toisistaan.
- silta - yksittäinen kaari, joka erottaa verkon osat toisistaan.
- vikasietoinen verkko - jokaista verkon osaa yhdistää vähintään 2 kaarta. ts. yhden kaaren poistamalla ei voida katkaista verkkoa
Sovitus
Sovitetaan joukot yhteen kriteereiden mukaan. esim yhdistetään opettajat ja kurssit siten, että kaikille kursseille on sopiva opettaja
Abtraktien tietotyyppien toteuttaminen
Abstraktit tietotyypit täytyy toteuttaa (implement)
Listan taulukkopohjainen toteutus
- ???
Puiden toteuttaminen
- ???
Verkkojen toteuttaminen
- ???
Joukkojen toteuttaminen
Hajautus - hashing
- Suljettu hajautus
- Uudelleen hajautus
- Satunnaistettu hajautus
- Fibonacci hajautus
Järjestäminen / Lajittelu
Kupla järjestäminen
- O(n^2)
- vaihdetaan päikseen väärät alkiot
Upotus järjestäminen / lisäysjärjestäminen
- O(n^2)
- viedään oikealle paikalle uuteen taulukkoon
Pikajärjestäminen - quick sort
- O( n log(n) )
- jaetaan kahtia ja järjestetään jonkun alkion mukaan oikealle ja vasemmalle, toistetaan kunnes kaikki paikallaan.
Kekojärjestäminen - heap sort
- O( n log(n) )
- alkiot prioriteettijonoon ja pois
Lomitusjärjestäminen - merge sort
- O( n log(n) )
- käänteinen pikajärjestäminen ??
Kaukalojärjestäminen - bin sort
- O( n + m ) - m = max arvo
- lasketaan esiintymisten määrät
Aikavaativuuden kertaluokka merkinnät
| Merkintä | Tarkoitus |
|---|---|
| Iso O | rajoittaa ylhäältä |
| Iso Omega Ω | rajoittaa alhaalta |
| Theta Θ | rajoittaa ylhäältä ja alhaalta |
| pikku o | rajoittaa aidosti ylhäältä |
| pikku omega ω | rajoittaa aidosti alhaalta |